Week 8: October 28, 2024
This blog is an ongoing project for Professor Ryan Enos' Election Analytics Course at Harvard College (GOV 1347, Fall 2024). It will be updated weekly with posts analyzing how different features impact the likelihood of Kamala Harris (D) or Donald Trump (R) winning the 2024 U.S. Presidential Election or winning specific states in the election. The blog will culminate in a final predictive model for the outcome of the general election.Context & Question
In this penultimate post, I will gear up to make a final state-by-state election prediction next Monday, November 4th. On this blog, I've looked at different predictors of candidate success (incumbency, ad tone, the value of the US dollar). I've also built a Bayesian Model to predict candidate success based on polling averages and updated by early voting returns. My final predictive model will be Bayesian and updated by early voting returns. To develop a prior probability, I plan to run a principal component analysis for each state. This will tell me what combination of features or variables the winner of each state tends to vary along--it's useful in a context with so many predictors and will allow me to incorporate more of the variables we've studied over the course of the semester. Since early voting is ongoing, I won't yet bring in early voting returns to this model; I'll incorporate them on Sunday, November 2nd.The Data
I've loaded datasets about polling averages, various economic conditions (GDP growth rates, nationwide unemployment rate, the consumer price index, and real disposable personal income), turnout rates, demographics, and ad spending. I tried to use as many state-specific variables as possible but some of these are constant across the nation. They're still important to include however because they may have greater *effects* in some states than others, or, in combination with other features, may predict the outcome of a state. To predict a binary winner from each state (Democrat or Republican) I will apply a sigmoid function to the line that explains variance of 2-party vote share along the first **two** principle components. It's worth noting the different amounts of data available for different predictors (e.g. some datasets have data going back to 1948, others to 1968, others to 2000, etc.). I will group data by state and election cycle and look at which principal components are best at predicting winners between elections. One challenge is that the principal components that best predict candidate success may change substantially over time, based on the priorities of Americans and the contexts in which they're living. Some of the data in this study goes back to 1968 and even 1948--it wouldn't be unreasonable to assume that the factors influencing voters today are different than those influencing voters back then.Results
The first step in a principle component analysis is to normalize each column of data by subtracting its mean and dividing by its standard deviation. This ensures that, since we are trying to see which predictors are most salient and amplify them in our prediction, the disparate scales do not make a difference. If we had data that where a "small" difference could be considered a value of 1,000 (like in ads spending for example), and DATA where a "large" difference could be considered 1,000 (like RDPI), then we'd unintentionally treat the small changes in ads spending the same as large changes in RDPI.## Importance of components:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5
## Standard deviation 4.1071496 3.3396968 2.36404621 2.10960949 1.88421786
## Proportion of Variance 0.2680222 0.1772163 0.08879767 0.07071211 0.05640945
## Cumulative Proportion 0.2680222 0.4452385 0.53403617 0.60474828 0.66115773
## Comp.6 Comp.7 Comp.8 Comp.9 Comp.10
## Standard deviation 1.84372945 1.61644308 1.48926088 1.33958700 1.24884858
## Proportion of Variance 0.05401123 0.04151552 0.03523962 0.02851225 0.02478045
## Cumulative Proportion 0.71516896 0.75668448 0.79192410 0.82043635 0.84521680
## Comp.11 Comp.12 Comp.13 Comp.14 Comp.15
## Standard deviation 1.17757577 1.08513922 0.94737263 0.90397582 0.84142497
## Proportion of Variance 0.02203268 0.01870943 0.01426039 0.01298384 0.01124917
## Cumulative Proportion 0.86724948 0.88595891 0.90021930 0.91320314 0.92445231
## Comp.16 Comp.17 Comp.18 Comp.19
## Standard deviation 0.81164337 0.717197658 0.674630990 0.634874670
## Proportion of Variance 0.01046695 0.008172734 0.007231397 0.006404211
## Cumulative Proportion 0.93491926 0.943091998 0.950323396 0.956727607
## Comp.20 Comp.21 Comp.22 Comp.23 Comp.24
## Standard deviation 0.590933527 0.539088818 0.5013082 0.491650549 0.43700088
## Proportion of Variance 0.005548389 0.004617536 0.0039930 0.003840632 0.00303427
## Cumulative Proportion 0.962275996 0.966893532 0.9708865 0.974727164 0.97776143
## Comp.25 Comp.26 Comp.27 Comp.28
## Standard deviation 0.414157368 0.403611371 0.366818436 0.346209057
## Proportion of Variance 0.002725338 0.002588311 0.002137923 0.001904437
## Cumulative Proportion 0.980486773 0.983075084 0.985213007 0.987117443
## Comp.29 Comp.30 Comp.31 Comp.32
## Standard deviation 0.320963792 0.297330277 0.276199771 0.264180983
## Proportion of Variance 0.001636823 0.001404649 0.001212094 0.001108901
## Cumulative Proportion 0.988754266 0.990158916 0.991371009 0.992479910
## Comp.33 Comp.34 Comp.35 Comp.36
## Standard deviation 0.259192592 0.2418755925 0.2370284684 0.2109740457
## Proportion of Variance 0.001067419 0.0009295521 0.0008926695 0.0007072089
## Cumulative Proportion 0.993547329 0.9944768813 0.9953695508 0.9960767597
## Comp.37 Comp.38 Comp.39 Comp.40
## Standard deviation 0.1933372708 0.1820839615 0.167562054 0.15975950
## Proportion of Variance 0.0005939103 0.0005267846 0.000446109 0.00040553
## Cumulative Proportion 0.9966706700 0.9971974545 0.997643564 0.99804909
## Comp.41 Comp.42 Comp.43 Comp.44
## Standard deviation 0.1529843745 0.1335264060 0.1265314806 0.106608331
## Proportion of Variance 0.0003718637 0.0002832853 0.0002543823 0.000180581
## Cumulative Proportion 0.9984209573 0.9987042426 0.9989586249 0.999139206
## Comp.45 Comp.46 Comp.47 Comp.48
## Standard deviation 0.0988967014 0.0967375312 0.0895954801 7.762810e-02
## Proportion of Variance 0.0001554008 0.0001486893 0.0001275445 9.574754e-05
## Cumulative Proportion 0.9992946066 0.9994432959 0.9995708404 9.996666e-01
## Comp.49 Comp.50 Comp.51 Comp.52
## Standard deviation 6.401733e-02 6.016315e-02 5.630253e-02 0.0502018318
## Proportion of Variance 6.511555e-05 5.751099e-05 5.036693e-05 0.0000400432
## Cumulative Proportion 9.997317e-01 9.997892e-01 9.998396e-01 0.9998796246
## Comp.53 Comp.54 Comp.55 Comp.56
## Standard deviation 0.0475398108 4.255698e-02 3.934794e-02 0.0327535835
## Proportion of Variance 0.0000359091 2.877606e-05 2.459991e-05 0.0000170454
## Cumulative Proportion 0.9999155338 9.999443e-01 9.999689e-01 0.9999859551
## Comp.57 Comp.58 Comp.59 Comp.60
## Standard deviation 2.246398e-02 1.947614e-02 2.539105e-05 3.463408e-08
## Proportion of Variance 8.017944e-06 6.026917e-06 1.024356e-11 1.905887e-17
## Cumulative Proportion 9.999940e-01 1.000000e+00 1.000000e+00 1.000000e+00
## Comp.61 Comp.62 Comp.63
## Standard deviation 2.634572e-08 1.277914e-08 0
## Proportion of Variance 1.102833e-17 2.594734e-18 0
## Cumulative Proportion 1.000000e+00 1.000000e+00 1
The principal component analysis of all states and races in the dataset indicates that 90% of the variance in 2-party vote share can be explained by the first 13 (out of 63) principal components. That goes a LONG way in reducing the dimensionality of the dataset, and still allows us to factor in economic data, turnout trends, demographic data, and polling averages into our prediction. To explain 99% of the variance, we only need to use 30 principal components. In the final prediction, I seek to repreat this PCA on a state-by-state basis, predict a probability that the Democratic Candidate will win, treat it as a prior, and then update it based on the latest early voting returns.
Bonus Content!
Since the PCA will be expanded on in my final election prediction, I wanted to provide a few relevant visuals and predictions to help us better understand the state of the 2024 Election. It's been a few weeks since I made predictions based on polling, and I wanted to practice pulling data from Fivethirtyeight, so here are some visuals and explanations about the current polling and approval ratings for candidates in the U.S. Presidential Election. The first is approval rating for Congress, the Supreme Court, the President, and the Vice President over the past 4 years. As we can see, Congress had a markedly lower approval rating than the other 3 institutions/politicians, which I wasn't expecting. This is surprising because congressional elections are held more frequently than presidential elections so I would think that the people expressing their approval/disapproval would have a say over congress members more often. The approval rating of the Supreme Court fluctuated most steeply, but if you look closely, you can see it fluctuate *with* the approval rating of Congress, rising and falling together. This may indicate something about how everyday Americans answering approval polls conceptualize the Executive Branch of government versus the Judicial and Legislative.##
## Attaching package: 'maps'
## The following object is masked from 'package:purrr':
##
## map
## `geom_smooth()` using method = 'gam' and formula = 'y ~ s(x, bs = "cs")'
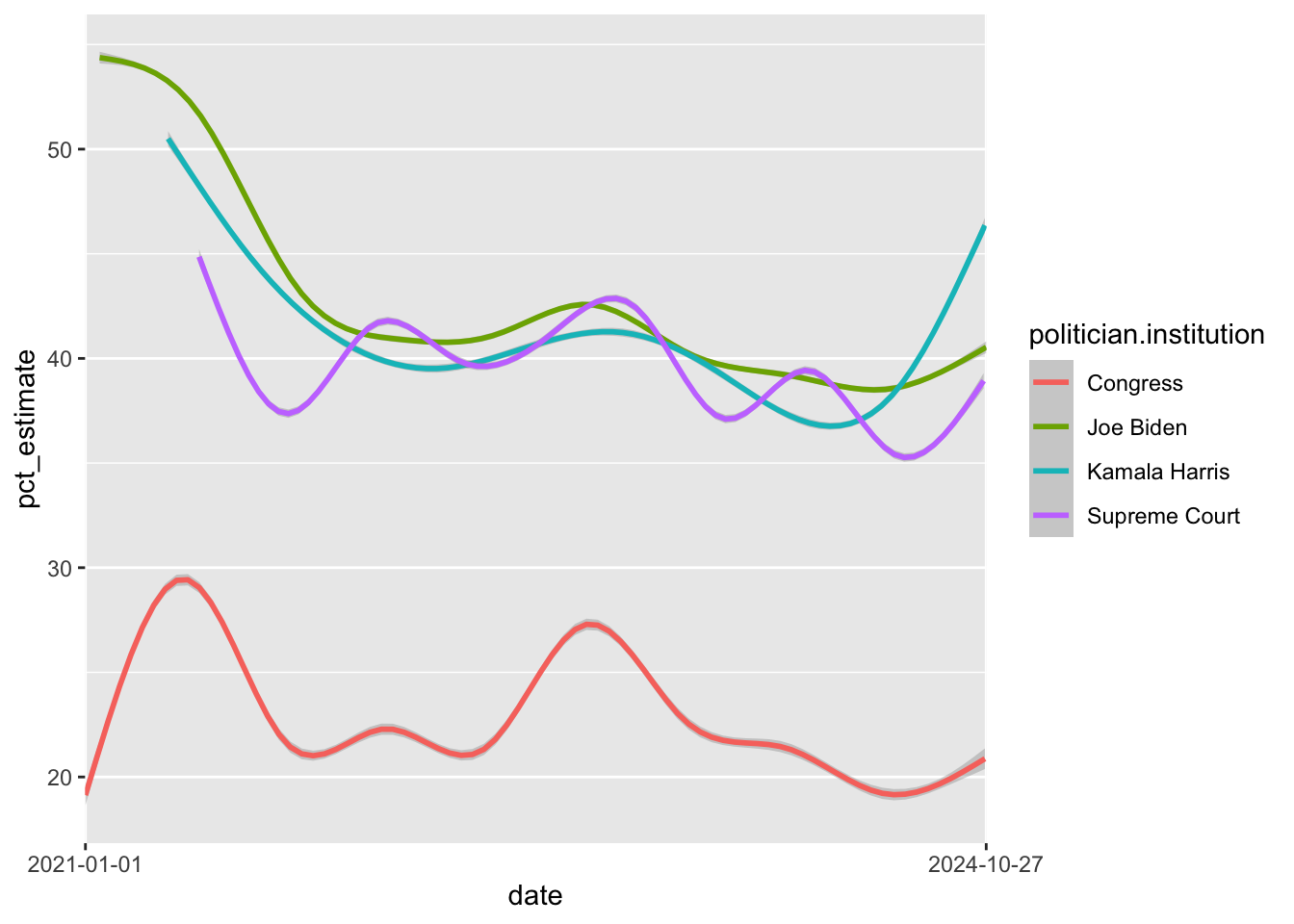
Unsurprisingly, the approval ratings for Joe Biden and Kamala Harris varied together. This makes sense because they make up the leadership of the same administration (or at least they are the most visible figures). However, we see the approval rating for Kamala Harris spike towards the end of the 4-year term… around when she began her presidential campaign. This is interesting because this poll is based on her work in office, not her campaign. So it suggests that, by running for the presidency, she developed a more favorable impression about her work in the Biden Administration, among everyday Americans. This could be the result of her having a greater platform to talk about the work, her gaining more visibility, or Americans becoming optimistic about her chance at the presidency.